Recommended by:
Top
20 UK science resources,
The Tutor Website
Recommended by:

Rated:

2010
Listed on the science,
engineering
and technology section of 
'providing you with access
to the very best Web resources for education and research, evaluated
and selected by a network of subject specialists.'
(Please note that intute closed in July 2011)
Section 1: Essentials (physical chemistry)
CHAPTER 1: ATOMIC
STRUCTURE
(Introduction and some topics arising)
NB This chapter has now been updated to improve
browser compatibility and to avoid the
need for non standard fonts.
Please
use the 'send email' link at the top right hand corner of this page to
report any problems.
QUICK SKIPS:
(Click on the 'back' arrow to get back to this quick skip section)
Mass number, atomic
number etc
Moles,
RAMs and Molar Mass
The
Avogadro Constant
The
importance of the Mole
More
on RAM, RMM etc
Isotopes
Mass spectrometer
Molarity and other
measures of concentration
Evolution of the
understanding of atomic structure
1.1.1. Two numbers give a remarkable amount of information about an atom. They are shown here for sodium (symbol Na):
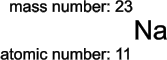
1.1.2. The mass number is the total number of protons and neutrons in the nucleus of the atom. The connection with mass is that protons and neutrons both have relative masses of 1. Since the electrons have negligible mass, the total number of protons and neutrons in a nucleus will be numerically equal to the relative atomic mass of the atom.
1.1.3. The atomic number is the number of protons in the nucleus of an atom, and even more information follows from this.
First, the number of neutrons in the nucleus can be simply calculated:
Mass number - Atomic number = number of neutrons
(12 in sodium)
Second, the number of electrons in the neutral atom can be deduced since it is equal to the number of protons. This makes sense, because protons each have a charge of 1+ and electrons each have a charge of 1-. Moreover, neutrons are (as the name implies) neutral.
1.1.4. The major characteristics of the atomic particles can be summarised:
| Relative mass | Charge | |
| proton | 1 | 1+ |
| neutron | 1 | 0 |
| electron | negligible | 1- |
Combined with the information in the table above, the information which can therefore be deduced from mass number and atomic number for sodium can be summarised:

and, moreover, relative atomic mass also = 23, the same as the mass number.
1.2. MOLES, RAMS, AND MOLAR MASSES
1.2.1. At this stage it is sensible to sort out some terminology which causes confusion well beyond this level of chemistry. If you are happy with the concepts of moles, RAMS and molar masses and with the two main measures of concentration (molarity and gdm-3), skip to the next chapter, but do so with caution (and only after looking at section 1.6 on mass spectra).
The ultimate cause of the confusion is historical. Because of the way our understanding of atoms has evolved, we have been left with some very clumsy concepts. If the history of everyday language had been similar, we might have been left with these definitions:
1.2.2. One dozen of any substance is the amount of substance which contains as many elementary units as there are eggs in 2 British supermarket boxes (exactly) of chickens' eggs.
1.2.3. The yolk constant is the constant of proportionality between amount of substance measured in dozens and the number of specified particles of that substance. It is represented by the symbol Y, and has a numerical value of 12; its unit is doz-1.
Fortunately, dozen has always simply been regarded as a name for the number 12. There is no need for Yolk Constants.
For all practical purposes, you won't go far wrong at this level if you consider mole as a name for the number 6.023 x 1023, just as dozen is is another name for the number 12, and don't worry too much about Avogadro constants.
Strictly speaking this is a little risqué. You should remain aware of the following definitions:
1.2.4. One mole of any substance is the amount of substance which contains as many elementary units as there are atoms in 12 grams (exactly) of pure carbon-12.
1.2.5. The Avogadro Constant is the constant of proportionality between amount of substance measured in moles and the number of specified particles of that substance. It is represented by the symbol L, and has a numerical value of 6.023 x 1023; its unit is mol-1.
In this context "specified particles" means molecules, atoms, ions, electrons, etc. To work out the number of molecules in 2 moles of oxygen we need to multiply by the Avogadro Constant:
|
No. molecules in 2 moles |
= 2 x L |
|
|
= 2 x 6.023 x 1023 |
|
|
= 12.046 x 1023. |
|
Similarly, to work out the number of eggs in 2 dozen we would need to multiply by the Yolk Constant (see above): |
|
|
No. eggs in 2 dozen |
= 2 x Y |
|
|
= 2 x 12 |
|
|
= 24. |
Here, all we are doing is multiplying by the number of eggs in 1 dozen. Similarly, in the preceding molar calculation we are multiplying by the number of molecules in 1 mole.
Fortunately, the controversy rarely arises. Moles are usually left as moles and not just because the large numbers are unmanageable:
1.3.
THE IMPORTANCE OF THE MOLE
1.3.1. The mole has not become important by chance. Its importance stems from the following fact. If an element has a relative atomic mass (RAM) of X, one mole of its atoms (i.e. 6.023 x 1023 atoms) will have an actual mass of X grams. In other words, the molar mass is numerically equal to the relative atomic mass.
Thus oxygen has a relative atomic mass of 16 and 6.023 x 1023 (one mole) of its atoms has an actual mass of 16g, i.e. a molar mass of 16g.
Note that relative atomic mass and molar mass are not the same thing. However, they are numerically equal. Here are the relevant definitions, plus a definition of relative molecular mass:
1.3.2. The relative atomic mass of an element is the ratio of the weigted mean mass of its atoms to 1/12 of the mass of a carbon-12 atom;
1.3.3. The relative isotopic mass of one isotope of an element is the ratio of the mass of one of its atoms to 1/12 of the mass of a carbon-12 atom;
1.3.4. The relative molecular mass of a compound is the ratio of the weighted mean mass of its molecules to 1/12 of the mass of a carbon-12 atom;
1.3.5. Molar mass is the actual mass in grams of 6.023 x 1023 (one mole of) specified particles of a substance (e.g. atoms of an element, molecules of a covalent compound etc.).
1.3.6. A word of warning on lazily learning definitions: It is tempting to learn definitions, but there are dangers in doing so. It is easy to learn a definition without fully thinking it through or understanding what it means. It is far better to understand a concept. If you understand a concept properly you should be able to describe that understanding in your own words. Such a description is actually a definition and a definition which you will be better placed to use and apply.
Whenever you see a question which asks you to define something, replace the words asking you to 'define.....' with words asking you to 'describe your understanding of .....'.
1.4.1. Relative molecular mass is also used (wrongly) for ionic compounds, but it is more correct to use the term, relative formula mass because ionic substances obviously do not contain molecules. They contain minimum groupings of ions, as specified by the chemical formula.
Thus it is the relative mass of an Na+/Cl- ion pair which concerns us in sodium chloride (NaCl). Similarly, it is the relative mass of the 2Na+/SO42- grouping in sodium sulphate (Na2SO4), and so on.
Certainly there is no shortage of terms and abbreviations used for these few concepts. Here are some of them:
1.4.2. Mole: gram atom, gram molecule (old names);
1.4.3. Relative atomic mass: RAM, Ar, atomic mass (sloppy), atomic weight (even worse);
1.4.4. Relative molecular mass: RMM, Mr, molecular mass (sloppy), molecular weight (even worse), relative formula mass (old but correct, and more correct than relative molecular mass when applied to ionic compounds);
1.4.5. Molar mass: MM, gram molecular mass (old name), gram formula mass (old name), atomic mass and molecular mass (bound to cause confusion), atomic weight and molecular weight (hopeless).
Note also that:
1.4.6. The empirical formula of a molecular compound is the simplest whole number ratio of atoms of each element present in the compund
whereas:
1.4.7 The molecular formula is the actual number and type of atoms of each element in a whole molecule
and:
1.4.8. The structural formula further shows how those atoms are arranged.
1.4.9. Note also that for an ionic compound only the empirical formula is relevant. Why?
1.4.10. Even the examining boards can be a bit lazy when it comes to applying these terms. The following 'magic formula' has been seen to appear in exam board mark schemes:
........................................Moles = mass / Ar
Why is this wrong? The answer it gives is the correct number.
The point is that using this (strictly incorrect) magic formula does nothing for our understanding and reinforces the continuing difficulties many students have with calculations.
To understand the calculation we need to understand that when calculating number of moles in a given mass of substance, we are trying to find out how many lots of 1 mole there are in that mass. We therefore need to divide the actual mass of 1 mole of substance into the given mass. The relative atomic mass may be numerically equal to the mass of one mole, but it is not the actual mass of 1 mole. It is a ratio of the (average) mass of one atom to 1/12 of the mass of a carbon-12 atom. The actual mass of one mole of substance is the molar mass. We therefore need to find out how many lots of the molar mass there are in the given mass. Applying this understanding we then arrive at our own conclusion that:
........................................Moles = mass / molar mass
rather than simply learning it parrot fashion without really understanding it.
1.4.11. More molar calculations
Molar calculations are a sticking point for many a student, though, hopefully, section 1.4.10 will have started to replace the magic formula, learn every answer approach with a simpler, more logical approach.
Most calculations involving moles follow the same simple 3 step pattern with start, middle and end:
Starting
information
(e.g. about substance X)
(e.g. mass and
molar mass)
...........↓
(Step 1)............................Middle
(Step 2)
No moles
of e.g. X...............
→ via simple molar ratio
→...............
No Moles
of e.g. Y
.....................................(e.g.
molecular formula or *stoichiometric equation)
...........................................Plus
further information
(e.g. molar mass). ↓ (Step 3)
End
= ...............................................................................................Answer
...........................................................................................(e.g. in this case mass of Y)
A good place to start is to find the substance for which you are given enough information to work out number of moles via step 1 - then you have found your starting information, identified your "substance X" and progressed a good way towards the answer.
If at that stage you are unable to see your whole way through, try finding your way through from more than one direction: it may help to identify your "substance Y", i.e. the substance about which the question requires the answer; and/or look for the simple molar relationship between your particular "X" and "Y" (simple molar ratio of X:Y), enabling you to complete step 2 and/or look for further information which will enable you to deduce via step 3 the information required by the question about Y once you have calculated the number of moles of Y. You should then be able to join the strands together.
Note that if you know the number of moles of a substance you can work out:
- Masses from molar mass (numerically equal to RAM, RMM etc.);
- Volume of a gas from the fact that one mole of any gas occupoies 24dm3 at room temperature (you do not need to remember this as it will be provided on the data sheet, in the data booklet etc.);
- Percentage yields and percentage atom economies (see chapter 19 section 19.4);
- Concentrations and
volumes for reactions in solutions (see this chapter, fig 1-3).
Of course, there can be deviations from the simple sequence above. The two most common deviations are:
- the stoichiometric relationship may involve a sequence of more than one reaction with more than one *stoichiometric equation;
- you may actually be asked to work out the simple molar ratio "in the middle" (e.g. in an equation or in a formula), having been given enough information about "X" and about "Y" to work out the number of moles of each.
*A stoichiometric equation for a reaction is the equation which gives the simple whole number ratios in which reactants react and products are produced. The word, itself, refers to the whole number ratio. Hence empirical formulae and molecular formulae are also stoichiometric (whole number ratios).
1.5.1. The relative atomic mass of chlorine is 35.5. This is because naturally occurring chlorine comprises two types of atom. Both types have 17 protons, as shown by the atomic numbers of 17. (In fact, it is the number of protons in an atom which ultimately determines its chemical properties and makes it the atom of a particular element.)
However, one type of chlorine atom has 18 neutrons and thus a relative atomic mass of 35, whereas the other type has 20 neutrons and thus a relative atomic mass of 37. Chlorine-35 and chlorine-37 occur naturally in a ratio of 3:1, so the average relative mass of the atoms is therefore 35.5.
The two forms of chlorine are known as isotopes.
1.5.2. Isotopes are different atoms of the same element, having the same numbers of protons, but different numbers of neutrons and therefore different relative atomic masses.
1.6.1. The mass numbers
of the
isotopes of an element
together with their relative abaundances may be found using a mass
spectrometer (see fig1.1).
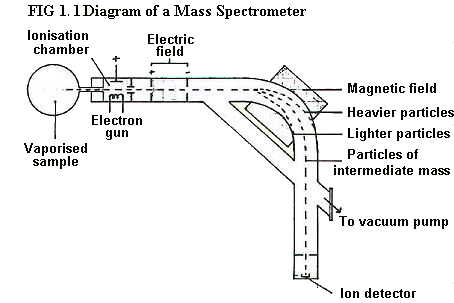
The vapourised element
enters the ionisation
chamber where it is
bombarded by a stream of high energy electrons. The collision between
atoms of the element and the high energy electrons causes one (or
sometimes two) of the atoms electrons to be knocked out forming
positive ions.
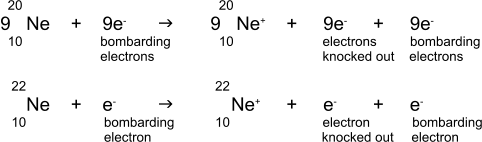
For example, neon comprises two
isotopes, neon-20 and neon-22 occuring in the ratio 9:1.
Thus considering 10 atoms of neon entering the ionisation chamber and
being ionised we could write:
The positive
ions so formed then pass through holes in parallel plates across which
an electric field is applied. The field accelerates the ions as a
single stream which next passes through a magnetic field. The magnetic
field deflects them according to their mass and charge.
It follows that the settings of the electric and magnetic fields can be
adjusted so that only particles of a particular mass/charge ratio will
hit the ion detector. (E.g. for neon, one combination of settings will
send neon-20 to the ion detector and another setting will send neon-22
to the ion detector.)
The actual mass/charge
ratio of a particular ion hitting the ion detector may be calculated
from the strength of the electric field, the strength of the magnetic
field and the arc of curvature. And, since most of the ions produced
will be 1+ ions, the masses of the different isotopes present may be
calculated.
Moreover, the relative proportions of
different ions hitting the detector is measured by the relative
currents produced in the ion detector. In the graph below (fig 1-2) the
heights of the peaks (or more correctly the areas under the peaks) give
a measure of quantities and the relative areas give a measure of
relative quantities of the different ions/isotopes present.
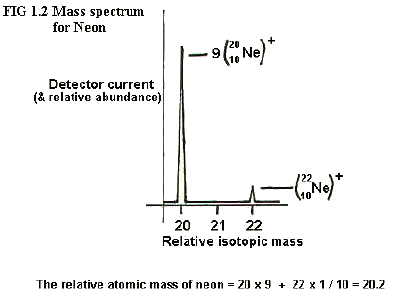
As shown in the
diagram, for neon the neon-20 and neon-22 isotopes are found to be in
the ratio 9:1 and this enables the relative atomic mass of neon to be
calculated as 20.2.
1.6.2. Note that the mass spectrometer can also be used to provide information about molecules. The first effect of the bombarding electrons is to knock an electron off the molecule producing a molecular ion with a 1+ charge. In the mass spectrum this will produce the peak with the highest mass/charge ratio (m/z value) i.e. the peak *furthest to the right.
E.g. ................CH3CH2CH3.......→.......CH3CH2CH3+.......+.......e-
At this level you will be asked to consider mass spectra only for ions with a charge of 1+ (z = 1), so the value of the peak furthest to the right will correspond with the relative molecualr mass of of the molecule under consideration: the first piece of useful information. In the case above a peak at m/z = 44 will be the peak furthest to the right.
The next thing the bombarding electrons will do is break the molecular ion into smaller fragments. For example in the case of propane above, a CH3 group may be broken off, leaving CH2CH3. This produces the expected peak at m/z = 29 corresponding with the CH2CH3 group, but many students never quite understand why there is not a corresponding peak at m/z = 15 corresponding with the CH3 group. The answer is that when the molecular ion fragments, the 1+ charge remains with the +CH2CH3 group and the ·CH3 group is an uncharged free radical so it is not detected in the mass spectrometer:
i.e. ................CH3CH2CH3+.......→.......CH3CH2+.......+.......·CH3
The resulting mass spectrum is called a fragmentation pattern in which
the other important thing to note is that the relative heights of the
peaks obviously gives an indication of the relative abundance of each
ion. A simplified mass spectrum for propance would look like this
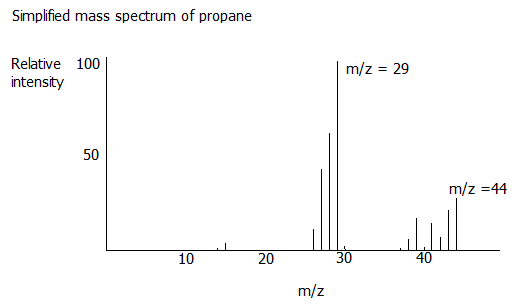
Can you work out what the other main peaks might represent?
*Note that there may be very small peaks to the right of the molecular ion peak owing to the presence of some carbon-13 in the molecule. Note also that chlorine will produce three molecular ion peaks at m/z = 70, 72 and 74, representing 35Cl35Cl+, 35Cl37Cl+ and 37Cl37Cl+. Be sure that you understand why the relative heights of the respective peaks in the mass spectrum of chlorine is 9:6:1, given the relative abundance of 35Cl : 37Cl is 3:1. There will also be peaks at m/z = 35 and 37 with relative heights of 3:1, representing the atoms produced by fragmentation. However, it is somewhat more dificult to predict their heights relative to the 70/72/74 peaks since this will depend on the proportion of chlorine molecules which fragment.
1.7
MOLARITY AND OTHER MEASURES OF CONCENTRATION
1.7.1. Having previously cleared up the mole, we can sort out molarity before returning to the subject of atomic structure. Molarity is a measure of concentration and should not be confused with the pure and simple mole. Nor should it be confused with another measure of concentration, gdm-3 (grams per cubic decimetre). And, whilst sorting out confusion, be warned: molarity also goes by other names.
When dealing with solutions, we can easily measure volumes. So, if we want to know how much dissolved substance (solute) there is in a particular volume of solution, it is useful to know how much solute there is in a standard volume of solution. That is, we need a measure of concentration.
The standard volume of solution which has been chosen is 1dm3 (1 litre). The amount of solute dissolved in 1dm3 can be given in grams or moles. This gives rise to two different measures of concentration:
1.7.2. Concentration in gdm-3 is the mass in grams of solute dissolved in 1dm3 of solution.
1.7.3. Concentration in moles dm-3 (molarity) is the number of moles of solute dissolved in 1dm-3 of solution.
Note also that a solution with a molarity of 2 (i.e. containing 2 mol dm-3)is also known as a 2 molar, or 2M, solution.
The interrelationships
between the measures of
amount of substance (moles and grams) and the measures of concentration
(molarity and gdm-3) are summarised in FIG. 1.3.
FIG
1-3 (Click on diagram to enlarge
on a new web page)
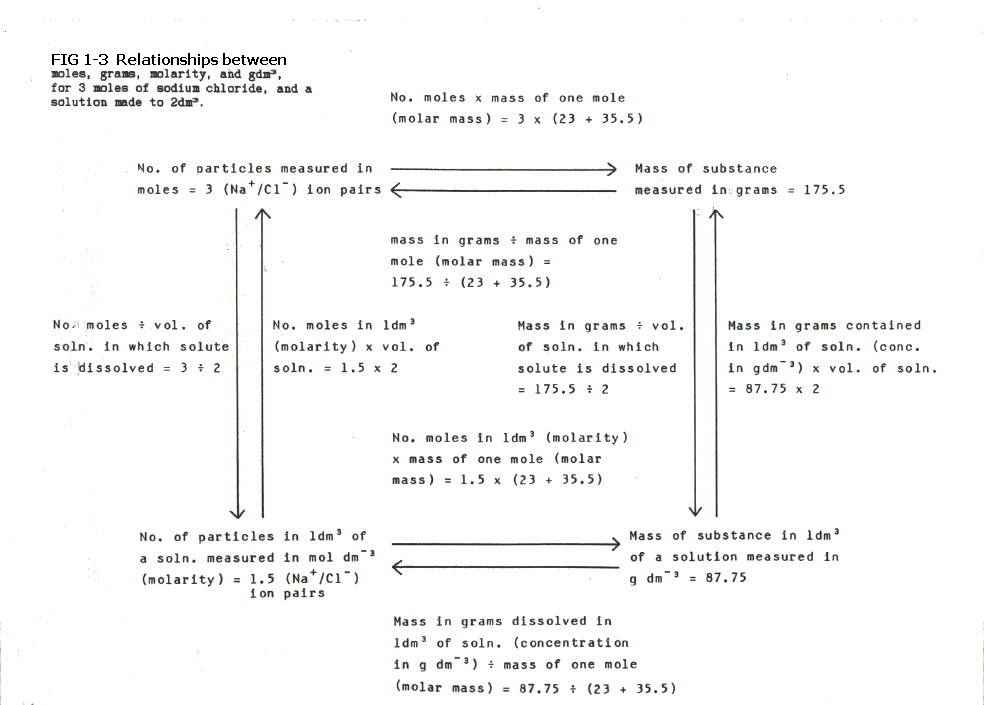
Think of it like this:
|
|
If
you find these calculations easy (given the information that a dozen
(12)
eggs has a mass of 780g): |
You
should find these easy (given the information that a mole (6.023 x 1023
ion pairs)
of sodium chloride has a mass of 58.5g): |
|
1 |
What is the mass of 6 dozen
eggs? |
What is the mass of 6 moles of
sodium chloride? |
|
2 |
How many dozen eggs are there
in 4680g? |
How many moles of sodium
chloride are there in 351g? |
|
3 |
If you have 6 dozen eggs in 3
bags, how many dozen eggs are there in *each bag? |
If you have 6 moles of sodium
chloride in 3 dm3 of solution, how many moles
are there in each dm3 of solution (i.e. what is
the molar concentration)? |
|
4 |
If you have 4680g of eggs in 3
bags, what mass of eggs do you have in *each bag? |
If you have 351g of sodium
chloride in 3 dm3 of solution, what mass is
there in each dm3 of solution (i.e. what is
the concentration in g dm-3)? |
|
5 |
If you have 2 dozen eggs per
bag, what mass of eggs do you have *per bag? |
If you have 2 moles of sodium
chloride per dm3, what mass of sodium chloride
do you have per dm3? |
|
6 |
If you have 1560g of eggs per
bag, how many dozen eggs do you have *per bag? |
If you have 117g of sodium
chloride per dm3, how many moles of sodium
chloride do you have per dm3? |
|
7 |
“Concentration”
measured in amount of substance (eggs) per bag: |
Concentration measured in
amount of substance (sodium chloride) per dm3: |
*Assuming
the eggs are evenly distributed
amongst the bags.
(Of
course, in a solution the ions are evenly distributed.)
Note
that
the calculations on line 1 are the same as the calculations on line 5,
except
that on line 5 you’re doing the calculations for amounts contained in 1
bag or
in 1 dm3.
Note also that the calculations on line 2 are
the same as the calculations on line 6,
except that on line 6 you’re carrying out the calculations for amounts
that
happen to be contained in 1 bag or in 1 dm3.
It can sometimes be useful to have an historical persepctive on the development of ideas. The concept of the atom arguably goes back to the times of ancient Greece. The word, itself, is derived from the Greek word, atomos, meaning indivisible. The ancient Greek philosopher, Democritus (c. 460 BC - c. 370 BC), is thought to have been the first person to suggest that if a substance was divided into smaller and smaller particles, eventually you would be left with particles of that substance which could be divided no further. It is possible that this idea originated with Democritus's mentor, Leucippus, but what makes it remarkable as an idea is that the ancient Greeks were unable to test it by experiment or observation.
Perhaps, then, it is not surprising that it was the early 1800s AD before this idea was developed further - by the English chemist, John Dalton. It was John Dalton who, based on experiments, suggested that:
1.
Elements
are made of (*unique) atoms, *i.e. the atoms of a particular element
are the same as each other, but different from those of any other
element.
2. Atoms cannot be broken down into smaller
pieces (indestructible).
3. Compounds are made from two or more different atoms joined together.
4. In chemical reactions atoms rearrange.
Dalton believed atoms to be indvisible solid spheres, but in 1897 J. J. Thompson discovered the electron. This suggested that the atom was not indivisible and a model of the atom was developed called the plum pudding model in which electrons (plums) sat in a positively charged 'pudding'. If you think this model sounds ridiculous, look at some of the models described in the next chapter and remember to think about what models are for.
However, the model was not consistent with experiments carried out in 1909 by Ernest Rutherford and his students, Hans Geiger and Ernest Marsden. They fired positively charged alpha particles at thin sheets of gold foil. They found that most of the alpha particles passed through, whereas a plum pudding model would have predicted that most of the alpha paritcles would have been slightly deflected by the positively charged puddings. Rutherford therefore developed the nuclear model of the atom (similar to Model 1 in the next chapter, but without the refinement of **shells) in which a tiny positive nucleus at the centre of the atom is surrounded by a cloud of negative electrons. Since most of the atom in this model is empty space, it is consistent with most alpha particles passing through the gold foil and only a very tiny number being deflected backwards by collisions with the nuclei.
**It was Neils Bohr who came up with the idea of shells to account for the realisation that negative electrons in a cloud around the nucleus, as suggested by Rutherford's model, would quickly spiral down into the positive nucleus. Bohr therefore proposed that the electrons existed in shells or orbits of fixed energy.
Experiments by further scientists showed that not all the electrons in any one shell had the same energy and the concept of sub-shells was born. Moreover, as will be seen in the next chapter, expermiental evidence then required sub-shells to be further divided into orbitals. However, as will also be seen in chapter 2, the accuracy of a model is not the only criterion against which it should be judged.
1.9. QUESTIONS
1) If an element, X, has an atomic number of 35, and one mole of its atoms has a mass of 80g, deduce the following quantities for the element:
i) relative atomic mass
ii) probable actual mass (in grams) of one of its atoms;
iii) probable mass number of one of its atoms;
iv) number of protons in each atom;
v) number of electrons in a neutral atom;
vi) mass of X2 molecules which must be dissolved in 1dm3 of
of tetrachloromethane to produce a 1 molar solution.
2) Why has the word "probable" been used in parts ii and iii of question 1? (Clue: see section 1.5. if you get stuck.)
3)
What pieces of information in section 1.1 have been used to deduce:
i. the
number of electrons in a neutral atom;
ii. the
relative atomic mass?
Unless otherwise
stated, all materials in this web version of chapter 1 are © 2005
Adrian Faiers MA (Oxon) MCIPR

What
's the connection between a dozen eggs and a garden mole?

Answer: Not a lot, really,
but see Chapter
1