Recommended by:
Top
20 UK science resources,
The Tutor Website
Recommended by:

Rated:

2010
Listed on the science,
engineering
and technology section of 
'providing you with access
to the very best Web resources for education and research, evaluated
and selected by a network of subject specialists.'
(Please note that intute closed in July 2011)
Section 1: Essentials (physical chemistry)
CHAPTER 4: CHEMICAL
BONDING
NB This chapter has now been
updated to improve browser compatibility.
Please
use the 'send email' link at the top right hand corner of this page to
report any problems.
QUICK SKIPS:
(Click on the 'back' arrow to get back to this quick skip section)
Bonding and the Periodic Table
Electronegativity and
Electropositivity
Predicting
bond type plus definitions
Other types of bond
Characteristics
of the different bond types
Intermediate types
of bond and Fajan's Rules
Predicting
the number of bonds
The octet fable
Hybrid orbitals
Shapes of molecules
4.1. INTRODUCTION
4.1.1. When it comes to bonding, perhaps the most important section in chapter 2 was section 2.3.3.: it is essential to imagine the electrostatic forces involved in bonding. Energy is also a useful concept, but on its own, it does not always lead to such a clear picture of the way things are.
It is electrostatic attraction which holds atoms and ions together, not energy. However, complex energy calculations provide essential information (for example the shapes of atomic and molecular orbitals). We do not need to examine the calculations in detail, but we do need to include in our models the information they provide (section 4.8.).
Moreover, energy gives us a quantifiable measure of the forces. A measure which is easily determined from experiments (chapter 9). See also sections 6.1.1. and 14.4.2.v.
4.2. BONDING AND THE PERIODIC TABLE
4.2.1. Section 2.4.2. was also important preparation for this chapter.
There are few facts at this level which must simply be learned. However, you must be able to instantly picture the place in the periodic table of any element mentioned in your syllabus. If you have these positions stamped on your mind as the starting point for all your inorganic theory, there will be far fewer other facts that you simply need to remember.
Here are the elements whose positions you must know for the majority of specifications at this level (FIG. 4.1.):
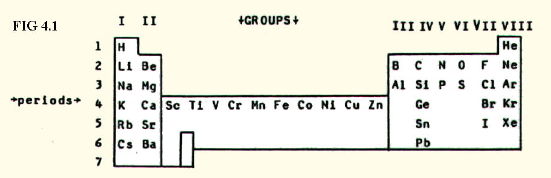
However, you will be given a periodic table in exams, so learn how to use it. A valuable part of inorganic chemistry is learning how to relate a vast mass of theory to two simple observations, and how to use the relationship to make predictions:
i) First observation: Physical and chemical properties of elements and their compounds follow largely predictable patterns down groups in the periodic table.
ii) Second observation: Physical and chemical properties of elements and their compounds follow largely predictable patterns across periods in the periodic table.
This is called periodicity. (Scroll up if you have just followed a link to periodicity or periodic patterns and trends.)
If you come to grips with this approach to inorganic theory, you will have mastered a powerful, and far more widely applicable, technique.
4.2.2. Patterns down a group: Changes down a group follow from the increasing number of electron shells down a group. This causes the outer electrons to become further (*and more screened from) the nucleus thus less strongly attracted.
Some changes are abbreviated as being due to the resulting increasing size.
(* Quantum mechanics reveals that, surprisingly, screening does not increase down a group as we might predict from the simple "shell" model of atomic structure. However, this fact is not widely accepted at this level, and the shell model prevails.)
4.2.3. Patterns across a period: Changes across a period follow from the increasing number of protons in the nucleus which have to hold only the same number of shells in place, offering roughly the same amount of screening. Thus the outer electrons become more strongly attracted and size decreases as a consequence in this case.
These changes are summarised as being due to increasing effective nuclear charge.
There are also more obvious changes associated with the increasing number of outer electrons.
4.2.4. Labouring the point: These patterns are fundamental. Inorganic facts should be learned only as examples of these patterns, or should at least be understood and related to each other in the light of the patterns. There are unlimited pieces of information you could learn.
Note also, that decreasing size across a period should never be given as a fundamental cause of any other pattern. Decreasing size itself follows from increasing effective nuclear charge.
This is so important that it is probably better not to use the concept of effective nuclear charge when explaining how patterns down a group tie together. (The nuclear charge down a group increases, but the effect of the nucleus on the outer electrons decreases.) It is best to refer back to the increased distance (and screening according to most examiners) of the outer electrons from the nucleus.
4.3. ELECTRONEGATIVITY AND ELECTROPOSITIVITY
4.3.1. The type of bonding between two elements can be conveniently predicted from their relative electronegativities.
In this context, electronegativity can be regarded as the ability of an atom to gain electrons and form negative ions. Conversely, electropositivity can be regarded as the ability of an atom to lose electrons and form positive ions. However, these days electronegativity is generally taken to mean Pauling's electronegativity, the strength with which the nucleus of a covalently bonded atome attracts the bonding pair of electrons. (See section 4.7.2.ii.)
Often the single characteristic of electronegativity is used: an electropositive element has a very low electronegativity.
Electronegativity follows group and periodic trends and changes.
4.3.2. Electronegativity down a group: Down a group, the outer electrons become further ("and more screened") from the nucleus. They therefore become less strongly attracted by the nucleus and more easily lost: the elements become more electropositive. It also becomes more difficult for the nucleus to attract additional electrons into the outer shell: the elements become less electronegative.
4.3.3. Electronegativity across a period: Across a period, the increasing effective nuclear charge means that the outer electrons are more tightly held, and that additional electrons are more strongly attracted into the outer shell: the elements become less electropositive and more electronegative.
4.4. PREDICTING BOND TYPE
4.4.1. By combining our understanding of the periodic table and of electronegativity, we can predict the type of bonding between pairs of elements.
4.4.2. Bonding between elements widely separated in the periodic table: Elements towards the left of the table and towards the bottom will tend to be the (least electronegative and) the most electropositive. They will be the most likely to lose electrons and form positive ions.
Conversely, those towards the top right hand corner of the periodic table will be the most electronegative (and least electropositive), and most likely to form negative ions.
These opposite types of element, which differ widely in electronegativity, are therefore most likely to form electrovalent (ionic) bonding with each other.
Definition: ionic bonding is the electrostatic attraction between oppositely charged ions which are arranged in a crystal lattice and which are formed by the transfer of electrons from one atom (giving positive ions) to another (giving negative ions).
Such
a transfer of
electrons to form ions can be represented for sodium chloride as
follows:
.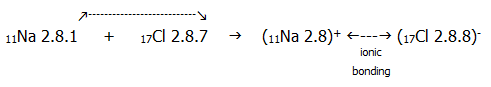
Or using dot and cross diagrams where dots and crosses represent individual electrons:
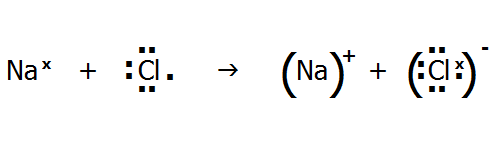
Note that we cannot define a single ionic bond in a lattice, because an ion is (strongly) attracted to all the surrounding (oppositely charged) ions in the lattice, as seen in the sodium chloride lattice (FIG. 4.2.):
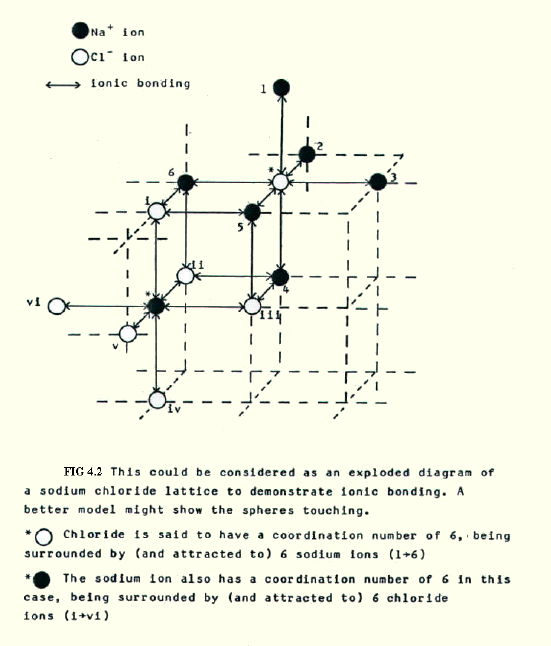
Other lattice arrangements are discussed in Chapter 5 (in more detail than you require for UK A Levels).
4.4.3. Bonding between elements close in the table:
i) The more electropositive elements: When two elements occur in the more electropositive region of the periodic table, neither is able to completely gain electrons from the other.
Moreover, neither is able to maintain sufficient control over the bonding electrons to form a covalent bond (section 4.4.4.).
In fact, those outer electrons which are available for bonding, form a cloud of electron density in which the resultant positive ions are arranged as a lattice. The bonding is metallic bonding, and it occurs between atoms of the same element as well as in alloys (see below).
Definition: metallic bonding is the electrostatic attraction of positive ions arranged in a lattice for the electrons in a single metallic bonding orbital which permeates the lattice (FIG. 4.3.)
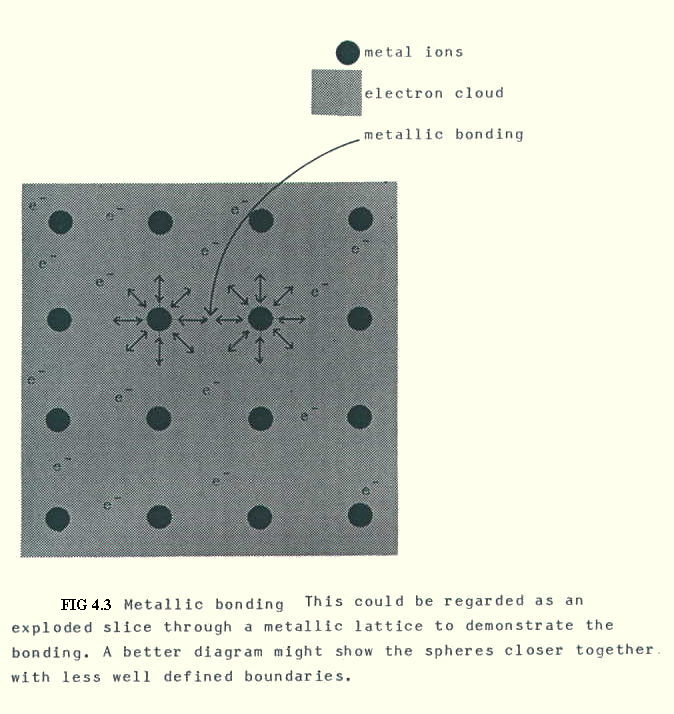
Some of the lattice arrangements are discussed in Chapter 5 (in more detail than you require for UK A Levels).
This type of bonding, unlike electrovalent or covalent bonding, does not require atoms of different elements to be present in fixed, whole number, (stoichiometric) ratios. True compounds are not formed, but alloys (section 18.7.). Alloys are intimate associations, somewhere between mixtures and compounds, in which a degree of separation can sometimes be achieved by physical means.
4.4.4. Bonding between elements close in the table:
ii) The more electronegative elements: When two atoms occur in the more electronegative part of the periodic table, neither will be able to completely lose control of electrons to the other.
Moreover, neither is able to lose sufficient control over the available bonding electrons to form a metallic bonding orbital.
In fact, the bonding electrons are held in a well defined space between the two bonding atoms. The more strongly they are attracted, the stronger the bond. The strength with which they are attracted can, in turn, be predicted from the patterns described in 4.2.2. above. It also follows that shorter covalent bonds tend to be stronger.
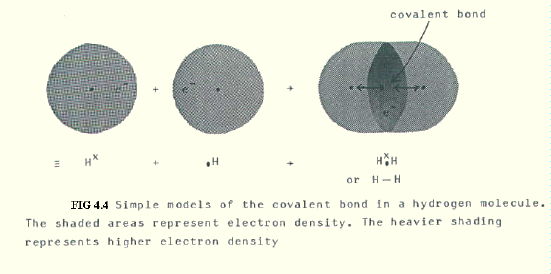
The precise definition of a covalent bond may surprise you, because at this stage it is important to emphasise that all bonds are forces of electrostatic attraction. Too often, covalent bonds are made to sound like diplomatic pacts based on an agreement between two atoms to share a pair of electrons.
Definition: A covalent bond between two atoms is the electrostatic attraction of the two nuclei for a shared pair of electrons in a bonding orbital formed by the overlap of two singly occupied atomic orbitals (or, in the case of a dative covalent bond, sometimes known as a coordinate bond, formed by the overlap with a vacant orbital of an atomic orbital containing a pair of electrons).
Note that for the first time we have been able to define a single bond. Note also that the key difference between one type of bond and another is where the electrostatic forces occur. All bonds are electrostatic forces of attraction between positive charge and negative charge, and therefore (ultimately) between protons and electrons.
A simple example of a covalent bond is shown for hydrogen in FIG. 4.4.
The formation of a dative covalent bond is illustrated by the following example:
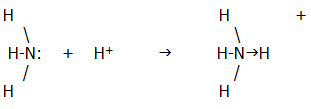
The arrow in the ammonium ion represents the direction in which the electrons have been donated to the bond. In practice, once formed, the new bond is indistinguishable from the other three covalent bonds. Dative covalent bonds are in general indistinguishable from ordinary covalent bonds. It is their history which differs.
Covalent bonding can be represented using dot and cross diagrams where each dot or cross represents an outer electron. E.g.
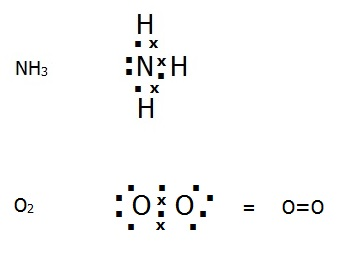
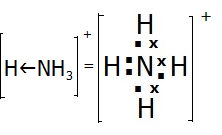
4.4.5. When two hydrogen atoms collide they do not always form a covalent bonding orbital like that shown in FIG. 4.4. For example, if the two atomic orbitals contain electrons with parallel spins, they will tend to repel each other. If they have opposite spins, their magnetic moments cancel out in a bonding orbital.
When repulsion occurs, it is sometimes said that an anti-bonding orbital has formed. This may seem like an elaborate construct for a non-event, and you will have to read elsewhere if you want to be convinced otherwise.
Certainly, at this level, the concept is likely to lead to meaningless statements like: "He2 molecules therefore do not exist because their formation is energetically unfavourable". This leaves unanswered real questions like, "What makes their formation energetically unfavourable?"
An explanation in terms of electrostatic forces would be closer to experience. If you could get down to atomic level and pull an electron away from an atom you would experience forces due to electrostatic attraction, not energy - at least, not in models which are easy to grasp!
The concept of energy is more useful in chemistry when considering something you would experience as energy, such as heat. It also provides a unifying concept, for example between electrostatic forces and heat or light. Moreover, it is useful as a tool for developing better models, as mentioned in section 4.1.1., and as we shall see in the section on hybrid orbitals (section 4.8.).
Energy is also an extremely important concept for checking predictions, and for making them when further explanation (or more detailed description) is unnecessary (section 14.4.2.v.).
4.5. OTHER TYPES OF BONDING
4.5.1. Hydrogen bonds: Hydrogen bonds are well defined by a description of the hydrogen bonds in hydrogen fluoride (FIG. 4.5).
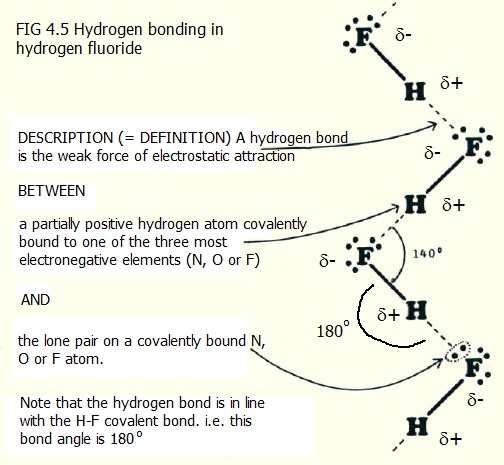
It is also helpful to include here another very important type of bonding, often excluded from specific mention in summaries of bonding. An Ion - dipole bond is the force of electrosatic attraction between the partial charge on one side of a polarised molecule and an oppisitely charged ion.
It is the type of force which accounts for the solubility of ionic compounds in polar solvents, despite the fact that ion - dipole bonds are very much weaker than the ionic bonding which needs to be broken for an ionic compound to dissolve. The explanation is that each ion has the potential to form a large number of ion - dipole bonds and it is the TOTAL strength of the large number of ion - dipole bonds which is of the same order of magnitude as the ionic bonding that needs to be broken.
Note that intermolecular bonding in the polar solvent must also be broken for an ionic compound to dissolve, but that these forces are relatively insignificant. By contrast, they are the significant forces which usually prevent simple covalent compounds from dissolving in polar solvents. Covalent compounds tend to dissolve in non-polar solvents where total strength of bonds broken in solute and solvent are likely to be of the same order of magnitude as the total strength of bonds formed in the solution.
As long as bonds made are similar in total strength to bonds broken, solubility is a possibility. [Although the deciding factor is the overall entropy change (see chapter 12), you will probably not have to think about it when considering most cases of solubility.]
4.5.2. London (dispersion)
Forces
, otherwise known as Van
der Waals bonds, are very weak
forces of electrostatic
attraction amongst instantaneous dipoles and induced dipoles.
At a given instant in time, the electron cloud surrounding even an inert gas atom may not be perfectly symmetrical. Thus one side will carry a relative positive charge and the other a relative negative charge. The separation of charge (instantaneous dipole) can be almost negligible in small atoms such as helium. In addition these instantaneous dipoles induce *dipoles in adjacent atoms and molecules (*induced dipoles).
Since the dipoles are very small, the forces which exist between them are also very small. Even at low temperatures, the random motion of group VIII atoms is vigorous enough to keep them gaseous. Moreover, on collision, repulsion between like charges is just as likely to occur as attraction between opposite charges.
However, as extremely low temperatures are reached, the random motion is not enough to break van der Waals attractions more often than they occur. Eventually, at low enough temperatures, the gas may liquefy, and the liquid may then even solidify. In energy terms, the kinetic energy is less than the bonding energy.
The larger an atom or molecule, the easier it is for dipoles to exist. In large atoms this is because the outer electrons are a long way from the control of the nucleus and it is therefore easier for instantaneous dipoles and induced dipoles to occur. Relatively simple large molecules (e.g. iodine) may solidify even at room temperature. It could even be argued that the distinction between the covalent bonds within the iodine molecule and the Van der Waals forces between them is becoming blurred for molecules the size of iodine and that the two types of bonding are tending to merge into metallic bonding. Iodine does, after all, have a metallic sheen normally associated with refelction by delocalised metallic bonding electrons. In contrast, helium must be reduced to 4K, and a pressure of 103 atmospheres must be applied, in order for solidification to occur.
Van der Waals forces are particularly important in determining the shapes which macromolecules such as proteins adopt (section 25.2.5.). Here, the large number of bonds compensates for their extreme weakness. This may also be the case between very large molecules. Note that in DNA, large numbers of hydrogen bonds are the important bonds holding the two strands together (section 25.4.6.).
4.6. BONDING CHARACTERISTICS
4.6.1. The decreasing order of strength of ion-dipole bonding and the three types of intermolecular bonding is:
ion
- dipole > hydrogen bonding > permanent - permanent
>> Van der Waals
.......................................................dipole..........dipole
4.6.2. The main type of bonding has effects on properties, as summarised in TABLE. 4.1.
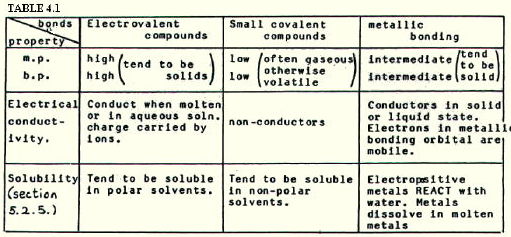
Note also that these intermolecular bonds may hold molecules in molecular lattices. Some of the lattice arrangements are discussed in Chapter 5 (in more detail than you require for UK A Levels).
4.6.3. The fact that ionic compounds have high melting and boiling points whereas covalent compounds have low melting and boiling points does not indicate that ionic bonds are stronger than covalent bonds.
The high melting and boiling points of ionic compounds do indicate that ionic bonds are strong i.e. the temperature must be high before ionic motion is vigorous enough to overcome the electrostatic forces of attraction.
However, covalent bonds are also generally very strong, but it is not these which break when small molecular compounds melt or boil. It is weak permanent dipole - permanent dipole or extremely weak Van der Waals forces between one molecule and another which break.
4.6.4. Note that hydrogen bonds are so much stronger than permanent dipole - permanent dipole bonds that ammonia, water and hydrogen fluoride have much higher melting and boilng points than expected from the trends in these properties of the corresponding hydrides below them in each group of the periodic table. For example, H2O is a liquid at room temperature whereas H2S is a gas. (See 14.3.1.)
Moreover, at 0oC and below the hydrogen bonds hold the molecules in a solid lattice (see 5.2.4.iv), forcing the molecules apart slightly and accounting for the slightly lower density of ice compared with water as well as for the fact that ice floats but with a high proportion of the ice (or iceburg) under water. This contrasts with the case of iodine mentioned above, which shows that even Van der Waals forces between molecules can lead to a simple molecular lattice and a simple molecular substance existing as a solid at room temperature.
Note also that the stronger a bond, the greater the energy needed to break it. Thus the value of the energy change associated with a particular change in state will refelct the strenght of the bonds broken.
4.6.5. We have already discussed in section 4.5.1 what accounts for the ability of ionic compounds to dissolve in polar solvents. Why do they not tend to dissolve in non-polar solvents?
Like so many questions in chemistry the first step is to frame the question and this invloves fully understanding the process to which the question refers. In this case the process involves breaking bonds in the substance which is dissolving (and in the solvent) and making new bonds between the dissolved species and the solvent. We can then start picturing those bonds and imagining their relative strengths.
Note that in the case of an ionic substance dissolving in a polar solvent, the bonding in the solvent is relatively weak (even in the case of water with its hydrogen bonding) and the fact that it must be broken in order for new ion - dipole bonds to form is not usually a significant factor.
However, when it comes to an understanding of why simple molecular compounds tend not dissolve in polar solvents, the strength of those bonds is key. The total strength of the solvent bonds that would need to be broken is usually far greater than the total strength of the new bonds that would form in any solution. Of course, the more polar a molecule is, the more likely it will dissolve in a polar solvent, because then total strength of the bonds broken and the bonds made get closer in magnitude. Hence, for example, simple alcohols dissolve in water (or is it the other way round?).
By contract, the total strength of bonds broken is of the same order of magnitude as total strength of bonds made when a simple molecular compound dissolves in a non-polar solvent. List the bonds broken and the bonds made and then explain why they are similar in magnitude.
4.6.6. It has been deliberate to talk in terms of 'similar in magnitude' rather than saying that the total strength of bonds made must be 'greater than' the total strength of bonds broken. As long as they are similar in magnitude, solubility exists as a possibility. A substance can dissolve even when the total strength of bonds made is less than total strength of bonds broken as long as the two are similar in magnitude. This is refelected in the energy change and the fact that the process of dissolving sometimes absorbs energy from the surroundings making the solution cool down. (Not the best example, but glucose tablets and some sweets have acooling effect in the mouth.)
The deciding factor in this case is entropy which will be discussed in chapter 12.
4.6.7. Electrical conductivity is discussed in table 4.1, itself. Note that high electrical conductivity in the molten state is the best single piece of experimental evidence that bonding is principally ionic (particularly important to keep in mind when considering the theoretical predictions in section 4.7). It is also evidence for the existence of ions, since it is mobile ions that are responsible for carrying charge. Even (pure) water, a molten, simple covalent compound, is a poor conductor by comparison, despite being a polar molecule which produces a low concentration of its own ions (H+ and OH-).
4.7. INTERMEDIATE TYPES OF BONDING
4.7.1. The three main types of bonding, electrovalent, metallic, and covalent are extreme cases. As often as not, bonding is intermediate between two types.
4.7.2. Electrovalent vs. covalent: There is an initial problem here of deciding whether to treat the bonding as ionic with covalent character or covalent with ionic character. This must be judged from an overall assessment of properties.
For example, any compound which conducts electricity in the molten state is more likely to be judged as principally ionic than it is to be judged as principally covalent, and vice versa.
i) Ionic bonding with covalent character: When two types of ion come together to form a compound, there is likely to be a high degree of covalent character when:
First,
the positive ion is: a) small
...................................b)
highly charged
Second,
the negative ion is: a) large
........................................b)
highly charged
(These empirical rules are known as Fajan's rules.)
It is predicatable that a small, highly charged positive ion will have a high surface charge density, and will tend to attract electrons away from the negative ion into a covalent bond.
It is also predictable that it will be easiest to remove electrons from negative ions when those electrons are a long way from the negative ion's nucleus, and when there is a large number of "extra" electrons in the outer shell.
ii) Covalent bonding with ionic character: When a largely covalent bond forms between elements of differing electronegativity (most cases), the electron pair will not be shared equally.
The more electronegative element will have a greater share of the bonding pair, as in the case of HCl molecules:
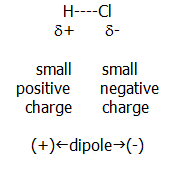
If it seems like fantasy to consider this molecular gas as partially ionic, remember that it dissolves in water to produce hydrated H+ and Cl- ions.
The greater the difference in electronegativity between two covalently bonded atoms, the greater is the ionic character, or polarity. Electronegativity in this context is strictly, Pauling's electronegativity, the strength with which the nucleus of a covalently bonded atom attracts the bonding pair of electrons (as explained in section 4.3.1.). This kind of electronegativity is measured on a scale of 0 - 4 with 4 being the score of the most electronegative element, Fluorine. The least electronegative element, Francium, at the bottom of Group I, has a score of 0.7.
If the difference in electronegativity is greater than 1.6, or so, the bonding can be predicted to be principally ionic, though this can be finally determined only by experiment. If the difference is less than A.4 - 0.5, the bonding can be regarded as effectively purely covalent. Anything in between is la polar covalent bond.
Sometimes the polarity of a molecule will be enhanced by its shape and the existence of lone pairs:

The assymetric ammonia molecule is polar. The symmetric molecule, aluminium hydride, is not because the dipoles cancel each other out. (Note that the words are 'symmetric' and 'assymetric'. 'Symmetrical' and 'assymetrical' are as wrong as saying 'ironical' instead of 'ironic'.)
Apart from discrete polar molecules, molecular solids may also exhibit ionic character. In fact, the mere existence of covalent molecules in a solid lattice is a step towards ionic character: the van der Waals bonding between molecules is becoming less distinguishable from the covalent bonding within the molecules (e.g. section 14.3.1.).
4.7.3. Covalent vs. metallic bonding: This is most relelvant to the case of pure elements and is well illustrated by changes down group IV (section 17.2.1) and group VII (section 16.2.1.) and by changes across the period from sodium to chlorine. We shall discuss the changes across a period here.
Sodium (LHS) is electropositive and forms clear-cut metallic bonding. Chlorine (RHS) is electronegative and forms diatomic molecules with a precise covalent bond between the two atoms.
From sodium to aluminium, the increasing effective nuclear charge (as well as the increasing number of electrons contributed by each atom to the metallic bonding orbital) causes the metallic bonding to become stronger. (Note that this is not the same as saying the bonding becomes become more metallic.)
By silicon, the effective nuclear charge is high enough to hold the bonding electrons in fairly concentrated regions of electron density on the axes between the nuclei i.e. the bonds are more covalent than metallic, but silicon still has a lattice structure more comparable with a metal than with the discrete molecules normally associated with covalent bonding.
Moreover, silicon has a metallic lustre, suggesting that the bonding electrons are diffuse enough to reflect light. Some of silicon's semi-conductive properties may also be considered as intermediate between metallic and covalent properties.
The higher effective nuclear charges of phosphorus and sulphur result in even more coavlent character. Discrete molecules are formed, P4 and S8, but van der Waals forces between one molecule and another are strong enough for both elements to be solids at room temperature.
4.8. PREDICTING THE NUMBER OF BONDS
4.8.1. Having predicted the type of bonding, it is necessary to predict the number of bonds (charge in the case of ions).
4.8.2. The octet fable: In its least controversial form the octet "rule" observes that atoms often end up with eight outer electrons when they form bonds. In its most controversial form it suggests that atoms form bonds in order to achieve this configuration. The configuration acquires the status of "stable octet" which is attributed with magical properties resulting from its similarity to the outer electron configuration of the "noble" gas atoms.
Perhaps it is the wishy-washy use of stability as an explanation which has allowed the continuation of the myth. In more cases than this, use of the word "stable" is an attempt to make "low energy" sound like a complete explanation.
The facts are even more disturbing. For one thing, in energy terms the octet is usually less stable than the electron configuration of the parent atom. This is indicated by the fact that even group I metal atoms (which are amongst the most able to lose electrons and form positive ions with an outer octet) require energy to remove the outer electron.
It is true that Cl-, with its outer octet, is more "stable" than the parent atom (electron affinities are often negative) but this is not because forming negative ions achieves the octet.
This is clearly illustrated by oxygen. An O- ion is more "stable" than an oxygen atom. The first electron affinity is negative i.e. the ion has less energy than the parent atom and energy is given out as heat when it forms. However, when O- goes on to achieve the octet by forming O2-, energy is required.
Elements which form negative ions are elements with high effective nuclear charges, and this is "why" first electron affinities can be negative. However, when a second electron is added to O-, it is repelled by the negative charge of the ion and must be added to a small shell which already contains seven, negatively charged, electrons.
Note that we have found it necessary to explain energy changes in terms of electrostatic forces.
4.8.3. Rubbing it in: In addition to all this, there are plenty of cases where bonding does not result in an outer octet:
i) More than the octet: a) Electrovalent: Fe3+ has 13 outer
..........................................electrons in Fe2(SO4)3
......................................b) Covalent: Sulphur has 12 outer
..........................................electrons in SF6
ii) Fewer than the octet: a) Electrovalent: Pb2+ has 2 outer
............................................electrons in PbSO4
........................................b) Covalent: Al has 6 outer electrons
............................................in AlCl3
The situation is more involved than the octet rule implies. There are far more events occurring than merely the formation, or otherwise, of octets. It is convenient to tackle the problem in terms of a more detailed look at energy changes, and to refer to the electrostatic forces involved in order to understand them.
4.8.4. Predicting the charge on a positive ion: Obviously this step comes after deciding that a compound is electrovalent and after deciding which element constitutes the positive ion.
i) The charge on a positive ion is equal to the number of electrons lost by the parent atom.
An atom is unlikely to lose more electrons than it has in the outer shell because the next shell is closer to ("and less screened from") the attraction of the nucleus.
An atom is unlikely to lose fewer electrons than it has present in the outer shell. This is because complete loss of the outer shell electrons not only makes the ion more highly charged, but also makes it much smaller. The resultant ion will therfore *form a much stronger lattice (in aqueous solution, it will be much more strongly hydrated).
With respect to calcium, try to picture the events and imagine the changing electrostatic forces when calcium atoms react with oxygen atoms. Then try to imagine the even more complex events when calcium metal reacts with oxygen gas.
(*In energy terms, the much higher lattice energy compensates for the extra ionisation energies.)
ii) Exceptions: Unlike the octet rule, this approach provides a basis for understanding exceptions. For example, elements at the bottom of group IV can form 2+ ions as well as the expected 4+ ions (section 17.3.2.iii).
The behaviour of d-block elements can also be understood. They can lose penultimate shell electrons as well as outer electrons because there is little difference in the strength with which their penultimate d-electrons and outer s-electrons are held by the nucleus (section 2.4.3.).
4.8.5. Predicting charge on a negative ion: When an electronegative atom gains electrons to form negative ions it fills any singly occupied orbitals in its outer shell.
It is unlikely to gain more than this number of electrons, since this would involve attracting electrons into a shell further ("and more screened from") the attraction of the nucleus.
It is unlikely to gain fewer electrons, because filling the singly occupied orbitals increases the charge but results in a relatively small increase in the overall size of the ion. The resultant ion will therefore *form a stronger lattice than an ion which still has a singly occupied orbital.
With respect to oxygen, try to picture the events and imagine the changing electrostatic forces when calcium atoms react with oxygen atoms. Then try to imagine the even more complex events when calcium metal react with oxygen gas.
(* In energy terms, the extra lattice energy compensates for the extra electron affinity.)
[As well as being able to predict the charge on simple positive and negative ions as described, you should also become so familiar with ions such as NO3-, CO32-, SO42-, OH-, NH4+, Zn2+ and Ag+ that you do not even have to think in order to remember their names, formulae, or charges. Moreover, having worked out the charge on ions, you should be able to construct formulae for ionic compounds by understanding that ionic compounds have no overall charge. Hence, if, for example, one ion has a single charge and the other a double charge, there must be twice as many of the singly charged ions in the formula, e.g. Zn(NO3)2]
4.8.6. Predicting the number of covalent bonds:
i) Covalent bonds: Obviously, predicting the number of covalent bonds comes after deciding that the bonding is covalent. Covalent bonds are usually formed by the overlap of singly occupied atomic orbitals, and the number of singly occupied orbitals in atom gives a rough indication of the number of bonds it will form.
ii) Electron promotion: There are, as you will recall, complications. For example, carbon in its "ground state" has two singly occupied orbitals:
.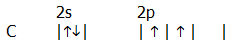
However, carbon almost exclusively forms four bonds. This is described in terms of a model in which one of the s electrons is promoted into the vacant 2p orbital, giving it four singly occupied orbitals:

The advantage of forming 4 bonds can be seen by considering methane. In each C-H bond the carbon and hydrogen nuclei are attracted to the high electron density of a bonding pair of electrons. This attraction is greater than the total attraction of a carbon nucleus for one of its outer electrons plus that of a hydrogen nucleus for its outer electron in an H2 molecule. In other words, the formation of two extra bonds outweighs the advantages of leaving carbon's s-electrons paired and closer to the nucleus than they would be in a p-orbital. Moreover, the electrons actually enter bonding orbitals rather than p-orbitals, as we shall see in section 4.8.
In energy terms, the two extra bond energies more than compensate for any promotion energy, and the H-H bond energy (c.f. section 17.3.1.ii.).
iii) d-orbitals: from the third period onwards, d-orbitals are available for electron promotion. Thus sulphur can form 2, 4, or 6 bonds:

In this electron promotion model, the number of bonds formed is dependent on the number of electrons promoted. This in turn depends on:
a) The sizes of the bonding atoms
b) The effective nuclear charges of the bonding atoms.
These can be deduced from the positions of the elements in the periodic table. Moreover, they affect two main aspects of covalent bonding which themselves have a bearing on the number of bonds formed:
a) First they affect the strengths of the bonds formed: then it can be predicted that the stronger the bonds, the larger the number likely to form.
b) Second, they affect the amount of space available for bond formation: then it can be predicted that the larger the bonding atoms relative to the central atom, the smaller the number of bonds likely to form, owing to lack of space.
Thus, referring back to sulphur, this element forms SF6 but not SCl6. This is predicatble for two reasons: First, fluorine's nucleus is closer to ("and less screened from") the bonding electrons than is chlorine's nucleus. Fluorine therefore forms stronger bonds than chlorine with sulphur. Second, chlorine's larger size means that there is less room for 6 of its atoms to fit around the small central sulphur atom (FIG. 4.17.)
You are likely to develop a feel for this kind of reasoning only after considering a good number of examples. Note also:
c) Multiple bonding reduces the number of bonded atoms required to form the higher oxidation states.
iv) Dative covalent bonds: a final complication is that orbitals containing pairs of electrons may be involved in dative covalent bond formation by overlap with vacant atomic orbitals.
Moreover, singly occupied orbitals may become available for dative bond formation by spin-pairing:
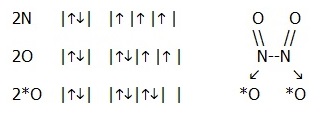
It is possible to predict the liklihood of dative bond formation from its strength and the amount of room available, and thus from sizes and effective nuclear charges of the bonding atoms. Hence (ultimately) the prediction can be made from the positions of the bonding elements in the periodic table. Again you will develop a feel for this after considering a large number of cases.
In the N2O4 molecule cited above, it is found that in practice all the N-O bonds are equivalent. This emphasises the fact that we are using a only partially correct model in order to make predictions. The model is developed by considering one more piece of bonding theory, hybridisation.
4.9. HYBRIDISATION
4.9.1. The shapes of atomic orbitals come from the solution of complex wave equations. Such calculations also allow shapes to be assigned to bonding orbitals, and they rely heavily on energy considerations.
The wave equations are simplified by considering only the predicted shapes of orbitals which atoms could theoretically use to form bonds. Quantum mechanists can actually calculate the space around a nucleus in which an electron will most probably occur (FIG.2.3.). The shape is a direct function of the orbital's energy, and this can change if hybridisation is included in the quantum mechanical calculations.
Despite the useful outcome of these calculations, it is not wise to be generally bullied by mathemeticians. A cynic might say that they resort to mathematical models because they have as much difficulty understanding reality as we have understanding them. Mathematical models must, as they are here, be related to reality. The calculated shape of an orbital is very useful for developing the models we use to describe atoms and molecules.
4.9.2. Why we need the concept of hybrids: Even when carbon is described as having promoted its 2s electron into the vacant 2p orbital, it is not in an appropriate state to form bonds, according to our existing models. This is despite having four singly occupied orbitals.
According to our existing model, the four orbitals are not a convenient shape, nor are they conveniently arranged, to overlap with other atomic orbitals (FIG. 4.6.)
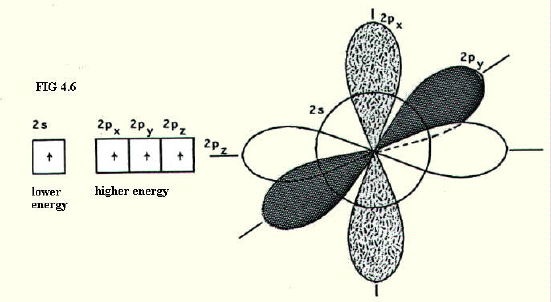
However, orbital shape is calculated as a function of energy. If the energy of an orbital were different from that considered as normal in a free atom, we would consequently predict a different shape. The energies of these orbitals would be different from normal if the distribution of energies amongst the orbitals were different from normal.
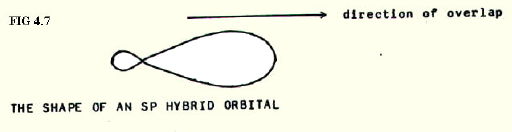
Moreover, the distribution of energy would be different from normal if the 2s orbital were equivalent in energy to one or more of the p-orbitals. As a predictive tool, it is suggested that this equalisation of energy does exist. It is known as hybridisation, and associated calculations describe some much more conveniently shaped (sp hybrid) orbitals (FIG. 4.7.).
There are three possibilities: sp1, sp2, and sp3 hybridisation.
4.9.3. sp3 hybridisation: In this case the s-orbital is considered as equivalent in energy to all three p-orbitals, giving four sp3 hybrid orbitals (FIG. 4.8.).
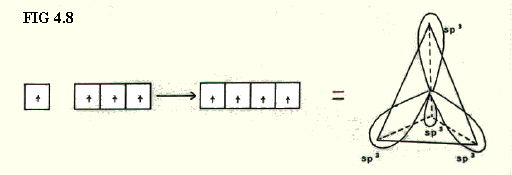
The four orbitals point to the four corners of a tetrahedron.
4.9.4. sp2 hybridisation: In this case the s-orbital is considered as equivalent in energy to two of the p-orbitals, giving three sp2 hybrids, and leaving one p-orbital with a higher energy (FIG. 4.9.).
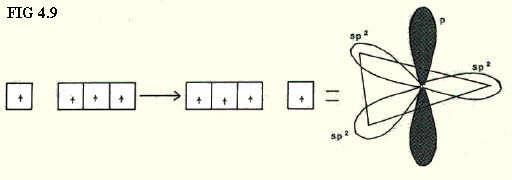
The three sp2 hybrids point to the three corners of an equilateral triangle.
4.9.5. sp1 hybridisation: In this case the s-orbital is considered as equivalent in energy to one of the p-orbitals, giving two sp1 hybrids, and leaving two p-orbitals with a higher energy, but with the same energy as each other (FIG. 4.10).
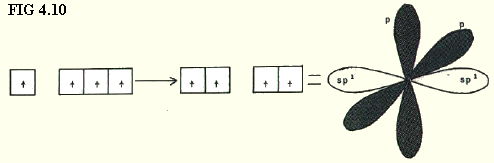
The sp1 orbitals are arranged linearly.
4.9.6. sp3 hybrids in methane (FIG. 4.11.):
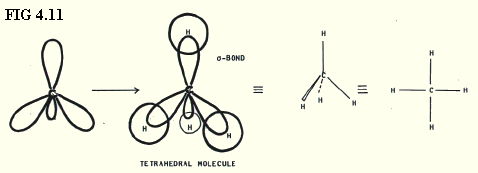
In an s-bond, the electron density is concentrated along the axis between the centres of the two bonded atoms.
4.9.7. sp2 hybrids in ethene (FIG. 4.12):
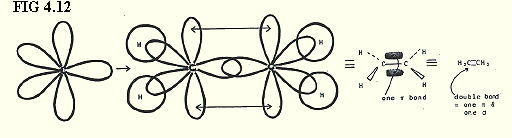
Note that the double bond contains two pairs of electrons. How would you represent this with a dot and cross diagram?
4.9.8. sp2 hybrids in buta-1,3-diene (FIG. 4.13.):
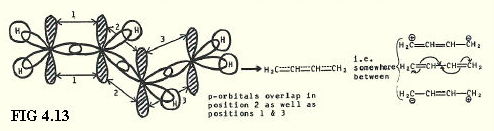
Electrons are said to be delocalised when they are not confined to the positions indicated in a simple bonding diagram, but are spread out by, for example, p-orbital and p-bonding system overlap.
4.9.9. sp2 hybrids in benzene (FIG. 4.14.):
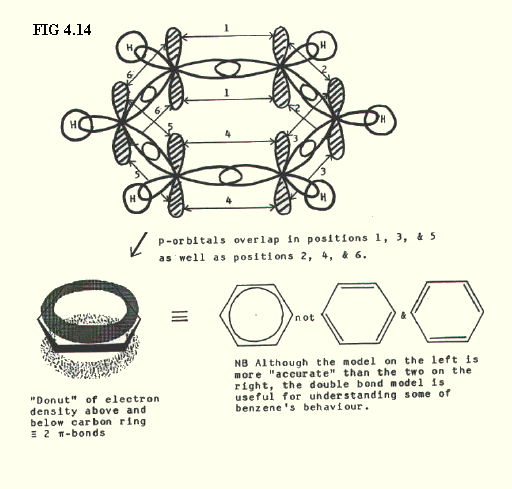
4.9.10. sp1 hybrids in ethyne (FIG. 4.15.):
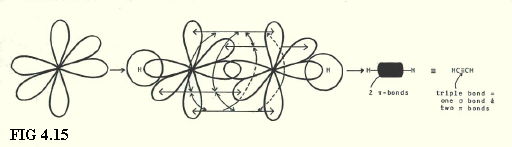
4.10. SHAPES OF MOLECULES
4.10.1. Hybridisation theory allows the shapes of molecules to be predicted. Shape may also be predicted by remembering that electrons in one bond will repel electrons in another. The repulsive effect of multiple bonds will be greater than the repulsive effect of single bonds.
Also, lone pairs of electrons will repel electron pairs in bonds, and repel other lone pairs, as well. Lone pairs exert a greater repulsive force even than multiple bonds.
Thus the shape of a molecule will tend to achieve maximum separation of bonding pairs of electrons and lone pairs, taking into consideration the relative strengths of the repulsive forces. These are summarised as decreasing in the order: lone pair > multiple bond > single bond. (This is a summary of, so-called, Sidgwick-Powell Theory). Some examples are shown in FIG 4.16 below.
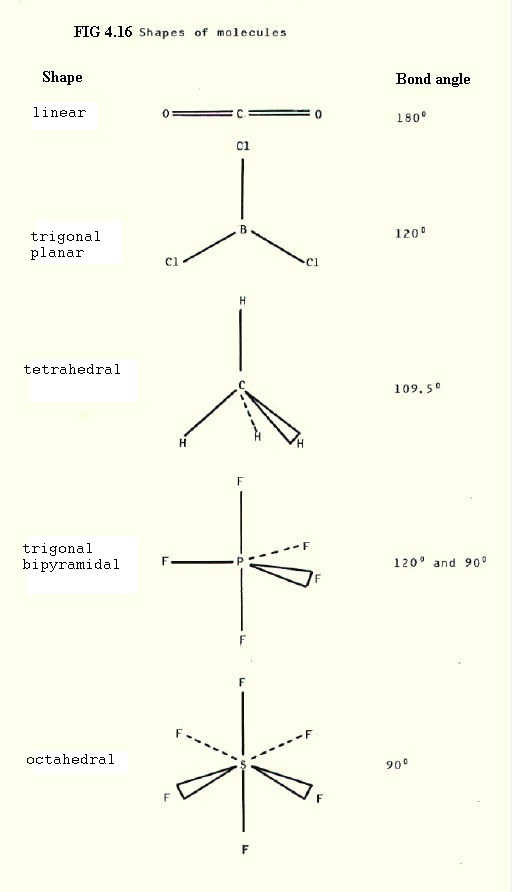
An interesting progression is the decreasing bond angle in the series:
CH4 → NH3 → H2O.
In methane the equal repulsion of the four bonding pairs of electrons achieves maximum separation with a bond angle of 109.5o. In ammonia, the lone pair repels the three bonding pairs more than they repel each other and this reduces the bond abngle by 2.5o to 107o. In water the extra repulsion of the two lone pairs reduces the bond angle by a further 2.5o to 104.5o
(Lattice arrangements in ionic compounds, metals, and molecular crystals are summarised in chapter 5.)
4.11. QUESTIONS
1) In chapter 2 we implied that it was dangerous to talk about causes, and about answers to the question "why?". How do you equate this with sections 4.2.2. and 4.2.3.?
2) What makes helium unable to form He2 molecules?
3) A small highly charged positive ion is more likely than a big positive ion with a single charge to form a strong ionic lattice? Comment.
4) How can the forces which exist in an ionic lattice be responsible for the existence of ions within that lattice? Answer the question with reference to the formation of calcium oxide from i) calcium atoms and oxygen atoms ii) calcium metal and molecular oxygen gas.
5) Why is the phrase "less screened from" placed in parentheses in this chapter?
6) Predict the simplest formulae of all compounds formed between the following pairs of elements, and predict the type of bonding found in each case:
copper and zinc, lead and oxygen, potassium and bromine, chlorine and bromine, oxygen and sulphur, sulphur and chlorine, beryllium and chlorine, strontium and sulphur, hydrogen and sulphur, phosphorus and bromine, phosphorus and fluorine.
In three cases, explain your reasoning.
7) Predict the shapes of SO2, CO2, AlCl3, NCl3, the [Cu(H2O)6]2+ ion, and SCl4.
8) Draw simple bonding structures for NO, NO2, N2O4, N2O5, SO32-, SO42-, S2O32-, S4O62-, S2O82-, and S2O72-.
Unless otherwise stated, all materials in this web version of chapter 4 are © 2007 Adrian Faiers MA (Oxon) MCIPR

What 's the connection between a dozen eggs and
a garden mole?

Answer: Not a lot, really, but see Chapter 1